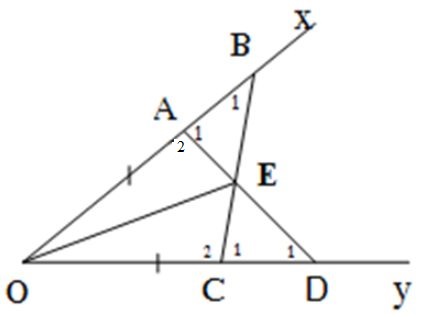
Bài 43. Cho góc xOy khác góc bẹt. Lấy các điểm A,B thuộc tia Ox sao cho OA
Bài 43. Cho góc xOy khác góc bẹt. Lấy các điểm A,B thuộc tia Ox sao cho OA Lấy các điểm C,D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh rằng: a) AD = BC; b) ∆EAB = ∆ECD; c ) OE là tia phân giác của góc xOy. Giải a) Xét ∆OAD và ∆OCB có: +) OA = OC (gt) +) \(\widehat{AOD}\) = \(\widehat{COB}\) (=\(\widehat{A}\)) +) OD = OB (gt) \( \Rightarrow \) ∆OAD = ∆OCB (c.g.c) Suy ra AD = BC (Hai cạnh tương ứng). b) ∆OAD = ∆OCB (cmt) Suy ra: \(\widehat{D_1}\) = \(\widehat{B_1}\); \(\widehat{A _{2}}\) = \(\widehat{ C _{2}}\) Mặt khác: \(\widehat {{A_1}} + \widehat {{A_2}} = {180^0}\) (Hai góc kề bù) \(\widehat {{C_1}} + \widehat {{C_2}} = {180^0}\) (Hai góc kề bù) Do đó \(\widehat {{A_1}} + \widehat {{A_2}}=\widehat {{C_1}} + \widehat {{C_2}}\) Mà \(\widehat{A _{2}}\) = \(\widehat{ C _{2}}\) nên \(\widehat{A _{1}}\) = \(\widehat{ C _{1}}\) AB = OB – OA (1) CD = OD – OC (2) OC = OA, OD = OB (gt) (3) Từ (1), (2) và (3) suy ra: AB = CD. Xét ∆EAB và ∆ECD có: +) AB = CD (cmt) +) \(\widehat{A _{1}}\) = \(\widehat{ C _{1}}\) (cmt) +) \(\widehat{B_1}\) = \(\widehat{D_1}\) (cmt) Suy ra ∆EAB = ∆ECD (g.c.g) c) ∆EAB = ∆ECD (câu b) => EA = EC. Xét ∆OAE và ∆OCE có: +) OA=OC (gt) +) EA=EC (cmt) +) OE là cạnh chung Suy ra ∆OAE = ∆OCE (c .c.c) Suy ra: \(\widehat{ AOE}\) = \(\widehat{ C OE}\) Vậy OE là tia phân giác của góc xOy.